MD5 is an older cryptographic hash function that is no longer considered secure for many applications. It turns data of any length into a fixed-length output. This output has a range of useful properties.
These properties make MD5 safe for data identification and for verifying whether data has been corrupted. However, the success of attacks against the MD5 algorithm mean that it’s no longer recommended for password storage. It should be avoided in situations where hackers may be able to modify data to commit attacks, such as in digital signatures and SSL certificates.
This article on MD5 will mainly focus on the background, security issues and applications of MD5. If you are interested in the underlying mechanics of the algorithm and what happens on a mathematical level, head over to our The MD5 algorithm (with examples) article.
The history of MD5
The first hash functions trace their way back to the work of Hans Peter Luhn in the 1950s. In 1958, he demonstrated a machine called Key Word in Context (KWIC) at an international conference. The KWIC was capable of automatically creating an index of articles that ranged in length from 500 to 5000 words, helping to speed up the process of classifying and organizing information.
Hash algorithms continued to advance in the ensuing years, but the first murmurs of cryptographic hash functions didn’t appear until the 1970s. Whitfield Diffie and Martin Hellman, the pioneers of the Diffie-Hellman key agreement scheme, were the first to identify the need for a hash that only functioned in one direction.
Later in the decade, a number of cryptographers began ironing out the basic details of cryptographic functions. Michael Rabin put forward a design based on the DES block cipher. Gideon Yuval published a 1979 paper called How to Swindle Rabin demonstrated the flaws in Rabin’s scheme, and how the Birthday Paradox could lead to collisions (two separate inputs resulting in the same hash value) that were originally unanticipated.
Ralph Merkle moved the development further by proposing requirements for collision-resistant hash functions. He also described the Merkle-Damgard construction, which was a way of building collision-resistant hash functions. This construction was later used in the construction of MD5 and its earlier iterations, as well as the currently used SHA family of hash functions. The idea of collision resistance was formalized by Damgard in 1987.
All of these developments eventually led to the Message Digest (MD) family of cryptographic hash functions, developed by Ronald Rivest, who is also renowned for providing the R in the RSA encryption algorithm.
The beginnings of the Message Digest family are a bit of a mystery as there is no publicly known MD1, nor much information about why not. The most likely explanation comes from the thesis of Bart Preneel, a Flemish cryptographer. As an industry insider, he may have had information that hasn’t been published elsewhere. Preneel wrote:
Rivest of RSA Data Security Inc. has designed a series of hash functions, that were named MD for “message digest” followed by a number. MD1 is a proprietary algorithm.
This implies that the very first message-digest algorithm was designed for an organization’s own use, and wasn’t released to the public. Rivest developed MD2 in 1989, but collisions were found by other cryptographers soon after. MD3 didn’t make it into the public realm either.
In section 18.10 of Bruce Schneier’s book Applied Cryptography it states that:
MD3 is yet another hash function designed by Ron Rivest. It had several flaws and never really made it out of the laboratory…
This was followed in 1990 by Rivest’s MD4. Attacks against the hash function were found relatively quickly, which led to the development of MD5 in 1991. MD5 was in use for much of the 90s and early 2000s, but over time, the attacks found against it became more and more serious.
The weaknesses of MD5 led to cryptographers recommending SHA-1 instead. SHA-1 was also found to be insecure over time. These days, we mainly use SHA-2, although there is also SHA-3. MD5 is still used for certain purposes, but it is strongly recommended against in situations where security is required.
What are hash functions?
Before we can get into the specifics of MD5, it’s important to have a solid understanding of what a hash function is.
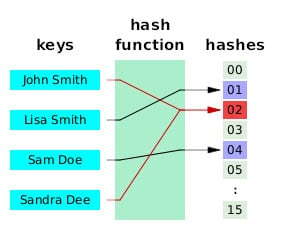
Hash functions take data of any size and transform it into a fixed-size value, known as a hash. Some people call them digests, hash values, or hash codes, but these are all just synonyms. These hashes are mapped into a hash table that orders the data, like in the image below. Simple hash functions are generally used for data storage and retrieval.
Hash table by Jorge Stolfi licensed under CC0
We will take a very simple hash function and explain it through an example. While hash functions can be used to map any type of data, including letters like in the picture above, we will stick with numbers to keep it easy.
Let’s say we have ten numbers that we want hashed:
- 76,541
- 884
- 9,826
- 22
- 474
- 19,465
- 56,490
- 25,738
- 64,829
- 7,432
You can play along at home with this hashing vizualization tool. Toward the bottom, you will see Choose Hashing Function, Collision Resolution Policy and Table Size. Select Simple Mod Hash, Linear Probing, and 10, respectively.
Enter each number in order, clicking Next when prompted. After entering the first number, you will be presented with the following:
Hash position = Input Value % Table Size
Hash position = 76541 % 10 = 1
Attempting to insert 76541 at position 1.
Inserting 76541 at position 1.
The first line, “Hash position = Input Value % Table Size”, simply lays out the formula for the simple modulo hash function. This operation is also often written as h (k) = k mod m, where:
- h (k) – The hash position for the input k.
- k – The input.
- mod – A modulo operation. These operations involve dividing the first number by the second. However, the answer isn’t the result that we would normally expect. The answer is whatever the whole number remainder is. As an example, 13 mod 4 does not equal 2.6. Instead, it equals 3. This is because 5 fits into 13 twice, with a remainder, of 3, our answer. In our example, the modulus (the divider, not the number being divided by) is the Table Size, which was 10. This makes all of the calculations relatively straightforward. When the modulus is 10, the remainder from the modulo operation will always be whatever the right-most digit is. The results of modulo operations are less predictable when other numbers act as the modulus. The sign for the modulo operation is often written as mod, but sometimes the % symbol is used instead.
- m – The size of the hash table. In this case, it is 10.
Therefore, the formula for the hash position of our first number, 76,541, is:
- h (76,541) = 76,541 mod 10
You can do this manually if you want, or enter the two inputs into this modulo calculator. If you do, the answer that you get is 1, which matches up with what our hash function told us above (76541 % 10 = 1).
If we go back to the four lines that the hashing visualization tool gave us, you will see that the third line says:
Attempting to insert 76541 at position 1.
Followed by the fourth line, which says:
Inserting 76541 at position 1.
The reason for this is that this modulo operation can only give us ten separate results, and with ten random numbers, there is nothing stopping some of those results from being the same number. If we are trying to create a hash table where each of these ten inputs are mapped to their own space in the table, we will run into problems if any of them have the same result.
This is why our hashing tool says that it is “Attempting to insert 76541 at position 1.” It can’t put a number in the hash table if there is already another number in that position. However, since this is the first calculation, there aren’t any other numbers in the table yet, so position 1 is free. Therefore, it can successfully insert “76541 at position 1.”
If you input the next few of numbers from our list, you will notice the hashing tool running the hashing operation in a similar manner as above:
Hash position = 884 % 10 = 4
Attempting to insert 884 at position 4.
Inserting 884 at position 4.
Hash position = 9826 % 10 = 6
Attempting to insert 9826 at position 6.
Inserting 9826 at position 6.
Hash position = 22 % 10 = 2
Attempting to insert 22 at position 2.
Inserting 22 at position 2.
It’s not until the fifth input, 474 that we notice something different:
Hash position = 474 % 10 = 4
Attempting to insert 474 at position 4.
Attempting to insert 474 at position 5.
Inserting 474 at position 5.
The first line tells us that the h (474) = 4. You can double check this yourself by inputting 474 mod 10 in the modulo calculator linked above. The answer is definitely 4, but the hash position of 4 is already occupied by the result of our second hash calculation:
h (884) = 884 % 10 = 4
Because the position is already occupied, you will notice that the hashing tool says:
Attempting to insert 474 at position 4.
Attempting to insert 474 at position 5.
Inserting 474 at position 5.
This is basically the hashing tool telling us that it tried to put h (474) in position 4, but it was full. Because of this, it decided to try and put it into position 5 instead. Position 5 was empty, so 474 got put into position 5 of the hashing table.
The hashing tool decides this based on linear probing, which we selected as the Collision Resolution Policy when we first set up the parameters for this hash table. A collision resolution policy is exactly what it sounds like, a set of procedures for the hashing tool to follow when there is a collision, which basically means when two separate inputs have the same hash position.
Our selection, linear probing, addresses collisions by searching for the next free location in the hash table. The hashing tool attempted to put 474 at position 4, but there was a collision, so the tool followed the collision resolution policy of linear probing and tried to insert 474 into the next slot, position 5. Position 5 was empty, so 474 was ultimately placed at position 5, even though h (474) = 4.
Filling out the rest of the hash table
If you continue inserting the rest of the ten inputs into our hashing tool, you will notice a few more collisions, most notably for number 19,465, where h (19,465) = 5. Position 5 is already filled, as is position 6, so 19,465 is ultimately placed at position 7, despite h (19,465) = 5.
Our final hash table ends up looking like:
- Position 0 – 56,490
- Position 1 – 76,541
- Position 2 – 22
- Position 3 – 7,432
- Position 4 – 884
- Position 5 – 474
- Position 6 – 9,826
- Position 7 – 19,465
- Position 8 – 25,738
- Position 9 – 64,829
The hash positions are substantially different from our initial order of:
- 76,541
- 884
- 9,826
- 22
- 474
- 19,465
- 56,490
- 25,738
- 64,829
- 7,432
You may look at the above and see it all as some kind of pointless endeavor. However, we have managed to map each of our arbitrary values (ranging from 22 to 76,541) to fixed positions in the hash table (ranging from 0 to 9).
This is extremely useful in terms of data storage and retrieval, because the hash table only takes up a little more storage space than the values themselves. It also allows access in a short, relatively constant timeframe, when compared to some of the alternatives for storage and retrieval.
The above is just an overview of how these hash functions work, serving as a stepping-stone to understanding how cryptographic hash functions work. This tutorial from the Virginia Tech Algorithm Visualization Research Group gives a more thorough description if you want to learn more about hashing and data retrieval.
What are cryptographic hash functions?
MD5 is a cryptographic hash function, which means that it is a specific type of hash function that has some of the same features as the one described above. Normal hash functions and cryptographic hash functions both map data of arbitrary size into fixed-size values, just like how 25,738 was mapped to position 8.
Just like with normal hash functions, the fixed-size values that result from cryptographic hash functions are also called hashes, digests, hash values, or hash codes.
However, cryptographic hash functions have a number of additional requirements:
- They are one-way functions – Which means that it is unfeasible to use the hash value to figure out what the original input was (with current technology and techniques). When a secure cryptographic hash function is used, it’s impossible to take the resulting hash and somehow deduce what the input must have been.
- They are deterministic – The same initial input will always yield the same hash value when it is put through the same hash function. When we put “They are deterministic” into this MD5 hash generator, it gives us a hash of 23db6982caef9e9152f1a5b2589e6ca3 every single time.
- Small changes to the input give radically different hash values – A small change in the input changes the resulting hash value so significantly that there no longer seems to be a correlation between the two. If we only change the final letter of the previous input from a “c” to a “d”, our input is still very similar. It’s now “They are deterministid”. However, when we put it into the same generator as before, it gives us a completely different hash value, 6b590a88650e7c5ee94fc8bda8e02000.
- It is unfeasible for two separate inputs to result in the same hash value – Secure cryptographic hash algorithms are designed in such a way that it is unfeasible for different inputs to return the same value. We want to make sure that it’s almost impossible for there to be a shared hash value between “They are deterministic”, “kjahgsdkjhashlkl”, “Once upon a time…” and any of the extraordinary number of other possible inputs. Of course, there are limitations to this. With infinite possible inputs, we would need a hash table that could store infinite hashes to prevent collisions. This would be impractical, so instead we settle for a compromise where it is extraordinarily unlikely for there to be a collision. We achieve this by making hashes incredibly large numbers.
- They are fast to compute.
What is MD5?
So far, we know that MD5 is a type of hash function, more specifically a cryptographic hash function. It has a bunch of seemingly strange properties that give it a variety of uses, however, due to its weaknesses, it is no longer considered secure for some of these purposes.
But what does the MD5 hash function actually consist of?
MD5 is a hash function that produces a 128-bit hash. This means that regardless of its input, the output is a fixed-length, 32 character hash, like this:
23db6982caef9e9152f1a5b2589e6ca3
MD5 hashes and hexadecimal
You will normally see MD5 hashes written in hexadecimal (16), which is an alternative numeral system. In everyday life, we use the decimal system which counts from zero to nine before going back to a zero again, this time with a one in front of it to indicate that this is the second instalment one through nine (10-19).
In contrast, hexadecimal numbers count from one to 16 before starting over again. Since we don’t have sixteen different single-digit numbers (we only have zero to nine, 10 is two digits), we add in the letters a, b, c, d, e and f to represent 10, 11, 12, 13, 14, and 15, respectively. This means that 16 in decimal can also be represented as 10 in hexadecimal
If you wanted to convert the hash from the previous section into the decimal number system that we are all familiar with, you would have to start from the right-hand side and multiply the number by sixteen to the power of zero. The right-most number was a three, therefore:
3 x 160 = 3 x 1 = 3
We would then move onto the next number, “a”, which is really just 10 in hexadecimal. This time we multiply it by 16 to the power of one:
10 x 161 = 10 x 16 = 160
Moving one space to the left, we have the number “c”, which is really just 12 in hexadecimal. Since it is the third digit from the right, this time we multiply it by 16 to the power of two.
12 x 162 = 12 x 256 = 3072
We continue moving one space to the left after each operation, performing the same calculation, but increasing the exponent (the number in superscript) by one each time. Once we have performed the operation for each of the digits, we add all of the outcomes together, which gives us the decimal equivalent of the hexadecimal number.
To save time, we will use a hexadecimal to decimal converter to do the work for us. When we enter in our hexadecimal hash, we find that:
23db6982caef9e9152f1a5b2589e6ca3
Is the hexadecimal version of:
47,662,232,879,966,347,151,498,352,140,906,032,291
The reasons why MD5 hashes are usually written in hexadecimal go beyond the scope of the article, but at least now you understand that the letters really just represent a different counting system.
The 128-bit hash value is only 32 characters long, because each character takes up four bits of information, and 128 divided by four equals 32. In other words, each byte of information (a byte is equivalent to eight bits) can represent two hexadecimal characters.
The MD5 algorithm
How does the MD5 hash function turn a phrase like “They are deterministic” into:
23db6982caef9e9152f1a5b2589e6ca3
How can it take inputs of any length, and always output a 128-bit hash?
How can it ensure that it’s unfeasible for any other input to have the same output (MD5 no longer does this because it’s insecure, but the underlying mechanism is still relevant)?
If you want to delve into every single step of how MD5 turns an input into a fixed 128-bit hash, head over to our The MD5 algorithm (with examples) article. It delves into the mechanics of what is happening and the many processes that are involved in changing the input into the hash. It all happens in an instant, but there is a lot of math going on under the hood of the MD5 hash function.
In this section, we will avoid going into the specifics, and instead cover the aspects of MD5 that make up its construction as a cryptographic hashing algorithm.
MD5 uses a one-way compression function, which is a type of cryptographic function that isn’t related to the data compression algorithms you may be more familiar with (for example, those used to make video and audio files smaller).
These one-way compression functions take two fixed-length inputs, and turn them into a single output of the same fixed length. As an example, two 128-bit inputs would lead to a single 128-bit output.
If you’ve been paying close attention, you may have realized that this goes against one of the main requirements of a cryptographic hash function, that they can take inputs of any length and always output a fixed size hash.
One-way compression functions can’t handle variable inputs, so MD5 gets around this by padding out its data, to make sure that it is always processed in 512-bit blocks of data. When the input is larger than 512 bits, it simply uses multiple blocks, padding out the final block with extra data to make sure it’s also 512-bit.
Collision-resistant cryptographic hash functions
A collision is when two different inputs result in the same hash. Collision resistance is incredibly important for a cryptographic hash function to remain secure. A collision-resistant hash function is designed in such a way that it is unfeasible for the hash of one input to be the same as the hash of a different input. When it is practical for attackers to produce two of the same hash from two separate inputs, this undermines the security of the cryptographic hash function.
For these so-called collision attacks to work, an attacker needs to be able to manipulate two separate inputs in the hope of eventually finding two separate combinations that have a matching hash. This contrasts with a preimage attack, where an attacker has to find an input that matches a specific hash value.
Collision attacks pose a significant threat in the cybersecurity world. We’ll run through an example to illustrate how two matching hashes for separate inputs could be problematic in the real world.
Let’s say that Evil Employee works at Firm A and is tasked with creating a $1,000,000 invoice to send out to Firm B. Evil Employee comes up with a scheme to make one version of the invoice legitimate, an invoice that essentially says “Firm B needs to pay Firm A $1,000,000”. Evil Employee then creates another evil version that says “Firm B needs to pay Evil Employee $1,000,000”.
Evil Employee messes around with both contracts, changing the wording, the fonts, the spacing and everything else. They go through countless combinations of both the legitimate and the evil version, until they finally come upon versions of both that have the same output when pushed through a hash function.
Evil Employee then shows the legitimate invoice to their boss. The boss signs it with their digital signature to prove that the invoice has been authorized. Evil Employee then switches the invoices up and sends the evil invoice to Firm B, alongside the boss’s digital signature that was made for the legitimate invoice.
Because the hashes for both the legitimate and the evil document are the same—they collide—when Firm B goes to verify the digital signature, they will never know that the switch took place. Evil Employee will end up with a cool $1,000,000 in their bank account and will already be in another country before anyone figures out what happened.
Hashes form a critical part of the digital signature verification process which underlies much of our online security. When a cryptographic hash function isn’t collision-resistant, it allows criminals to commit a wide range of fraudulent schemes that undermine the digital signature system.
Merkle-Damgard construction
As we have stated, the MD5 hash function involves one-way compression functions.
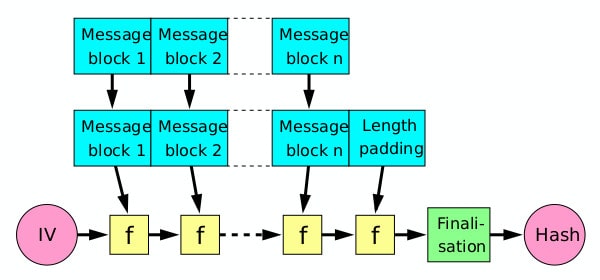
More specifically, the MD5 hash function features one-way compression functions with Merkle-Damgard construction. This is a design technique that aims to turn collision-resistant compression functions into collision-resistant cryptographic hash functions.
Merkle-Damgard construction relies on the formal proof that if the one-way compression function is collision-resistant, then so is the hash function that uses it. The Merkle-Damgard construction’s purpose is really just to extend a collision-resistant compression function and make it capable of taking variable-length inputs, rather than the fixed-size inputs that they normally handle.
This element of MD5’s design is one of the key components for turning a compression function into a cryptographic hash function that can take in any input, but will always return a fixed-length output.
Merkle-Damgard hash by David Gothberg licensed under CC0
If you familiarize yourself with the details of The MD5 algorithm (with examples) article, you will see that the MD5 algorithm is structured with similar Merkle-Damgard construction to that shown in the image above. The MD5 algorithm breaks up the initial input into fixed-sized blocks, processing each one through the compression function alongside the output of the prior round.
This property of the Merkle-Damgard construction was an important aspect of what made the MD5 hash function secure in the past.
MD5’s security weaknesses
As we have mentioned, MD5 is no longer considered a secure hash function. Its security woes began in the nineties, not long after it was first released. While it wasn’t a fatal blow to MD5’s security, Bert den Boer and Antoon Bosselars released a paper in 1993, which criticized the changes that were made in the upgrade from MD4 to MD5. Bosselars and den Boer found that they could create collisions for the MD5 compression function within MD5, but not for the MD5 function overall.
These collisions were termed pseudo-collisions in a paper published by Hans Dobbertin in 1996. Dobbertin’s paper discussed a more serious flaw in MD5. If an attacker were able to choose an initial starting value for the buffer rather than the one given by the algorithm, and was also able to choose two very similar but slightly different message inputs, then the attacker may be able to produce the same hash for both inputs.
Dobbertin’s paper showed a more worrying collision than the pseudo-collision documented by Bosselars and den Boer, but again, it didn’t break the overall MD5 function. Once more, it was a collision on the compression function rather than the overall MD5 function. While this was another worrying sign, the MD5 hash function was still considered secure at this stage.
The growing threat from MD5 collisions
Security researchers were becoming wary of MD5 hash function, but it remained in widespread use. It wasn’t until 2004 that researchers published a more serious collision. Xiaoyun Wang and Hongbo Yu’s paper How to Break MD5 and Other Hash Functions presented a method for finding collisions in the MD5 hash function within an hour.
The researchers’ technique involved finding a pair of message inputs that had specific mathematical relationships with each other. Using what was at the time a high-end server, they were able to find such collisions in as fast as 15 minutes. This attack was the first to show that collisions of the MD5 hash function as a whole were feasible.
It was followed in 2005 by a paper that demonstrated a collision in more practical terms. In Colliding X.509 certificates, Arhen Lenstra, Xiaoyun Wang and Benne de Weger showed that MD5 collisions could lead to two separate X.509 certificates with the same digital signature.
The security of the internet is based on trust in the Public Key Infrastructure, of which these certificates are a core component. The MD5 collisions made it possible for two separate X.509 certificates to both have the same signature from the issuer.
These certificates are critical in the security ecosystem, because they link an entity’s identity and their secret key. If two certificates can have the same signature, then it can be impossible to know which one is the true owner of the secret key. This poses a huge threat to the security of our online world.
Just a few days later, things began looking even worse for MD5. Vlastimil Klima published a paper detailing a method for discovering the first block that was supposedly 1,000-2,000 times faster than the one developed by Wang et al..
While Wang et al.’s team could find the second block much more rapidly, Klima estimated that the new method was three to six times faster overall. Klima’s paper states that the first collision could be found in eight hours on a humble 1.6 GHz notebook PC.
This attack was even more worrying, because not only could it be used for forging digital signatures, but it showed the attack was within the reach of the everyday hacker.
MD5 is broken
By the end of 2005, even MD5’s creator Ron Rivest was stating that the hash function was ‘clearly broken’.
In 2009, a preimage attack was proposed by Yu Sasaki and Kazumaro Aoki. However, this attack has a complexity of 2123.4, which is not even close to being feasible. No practical preimage attacks against MD5 have been discovered yet.
In 2010, researchers Tai Xie and Dengguo Feng published a collision with only a single block. Prior to this paper, only multi-block collisions had been found. Xie and Feng found two separate message inputs that yielded the same hash value. However, they did not publish the details of their technique, stating that they withheld them for security reasons. Another single-block collision was found by Marc Stevens in 2012.
While MD5 had been considered increasingly insecure after each publication, it wasn’t until 2011 that the Internet Engineering Task Force (IETF) published a new RFC advising updated security considerations. The RFC deemed that MD5 was no longer acceptable in situations where collision resistance was required, such as for digital signatures. However, it did still allow MD5 for hash-based message authentication codes (HMACs).
Despite the known security issues of MD5, the hash function was still widely implemented for several years after the update.
The applications of MD5
Cryptographic hash functions like MD5 are common in cybersecurity. They are most prominently used in various types of authentication and in digital signatures.
Earlier in the article, we listed out the many strange properties of cryptographic hash functions. These requirements (such as needing to be deterministic one-way functions) weren’t some kind of pointless intellectual exercise. Instead, these aspects have been chosen because they make cryptographic hash functions useful.
Let’s start by discussing a common yet controversial application of MD5, password storage and verification.
Cryptographic hash functions and password verification
Before we discuss how MD5 is used in the password verification process, let’s back up a little and look at the overall system.
You have dozens of different online accounts (hopefully with strong and unique passwords for each). When you create each account or change your password, you may assume that the website stores your password somewhere. How else could the website verify that the password you entered was correct?
Let’s assume for a moment that it does store your password. What would happen if an attacker busted into the website’s systems and stole the password database? Every single user’s account would be compromised, and users who rely on the same password for each of their accounts would be vulnerable across every site they log in to (this is why passwords need to be unique).
The risk of catastrophe from data breaches makes storing passwords a bad idea, no matter how good a website thinks its security is. Thankfully, cryptographic hash functions give us a much better option, and hopefully, all of your online accounts actually use them.
Instead of ever directly storing your password, websites can set up their password input fields to hash it immediately, and only ever store this hash. Whenever a user logs in, the password they enter is immediately hashed (again, never stored).
This hash is then compared to the password hash that the website has stored in its database. If the two hashes match, the website knows that the correct password has been entered, and it grants the user access.
The beauty of this system is that the site never needs to keep a copy of any user passwords, the only things it needs to store are the hashes. If this is the case, when a hacker breaks into the system and steals the password databases, it’s nowhere near as bad. This is because hashes are one-way functions and it is impractical to reverse them to figure out the input.
There are a number of caveats to the above point, including that a secure cryptographic hashing algorithm has been used, as well as salting, etc.. These caveats are far more stringent for MD5, because it is not considered secure as a standalone hashing algorithm for passwords. We will discuss this in more detail later.
Let’s demonstrate how the overall concept works by saying your password is “8Dnhf(3g&n2Jb5V!2G8Na^”. This hash calculator can play the role of the website that hashes and stores your password. When you enter a new password for the first time, the website immediately converts it to the hash and stores it:
80ddfe44955c5e3da8b2292463682f28
The website never stores your password. Each time you log in, you enter your input into the field and the site hashes it straight away. It compares this hash to the one it has stored on its servers. If the two match, it grants you entry into its systems. Again, the password itself is never stored.
If the website has the appropriate systems for processing and storing these password hashes, it doesn’t matter too much if an attacker (again, with caveats) steals the database. The attacker can try as hard as they want, but they won’t be able to figure out a sufficiently strong password from its hash (caveats).
They can try entering it in as the input to a hash calculator, but it isn’t going to work, because cryptographic hash functions are one-way functions. They can search all over the internet, and try every technique they find, but they will come back with nothing (caveats).
MD5 and password verification
MD5 is still used to store user passwords. As we mentioned, MD5 is now considered extremely insecure, especially for applications that require collision resistance. But what does this mean in the context of password hashing?
The fact that MD5 is vulnerable to collisions doesn’t really impact its security in the context of password hashing. This is because an attacker is only able to manipulate one of the inputs when trying to find a matching password hash. The other input has already been selected by the user (refer back to the Collision-resistant cryptographic hash functions section for further clarification of why collision attacks are suited to other scenarios).
When it comes to password hashing, it’s more important for the hash function to be preimage resistant, which MD5 still is. However, there are other factors that make MD5 unsuitable for password hashing. The algorithm is too fast and lacks a salt by default, which allows attackers to rapidly make millions or billions of password guesses.
The speed of the algorithm and the lack of a salt mean that short and uncomplicated passwords that have been hashed with the MD5 hash function are vulnerable to rainbow table attacks. They are also vulnerable to brute force attacks. If an attacker manages to steal a database of passwords hashed with MD5, the speed of MD5 allows them to rapidly guess passwords that match the hashes in the database.
Given that many people still use short or common passwords, MD5 password hashes may not take that long to guess. This presents a grave risk to many users, as evidenced by CynoSure Prime’s password cracking in the wake of the Ashley Madison data leak. The group was able to figure out millions of passwords in just a few hours, because the passwords and usernames were hashed with MD5.
MD5 hashes can be secure if a user has an incredibly long and strong password. They can also be secure when both salting and key stretching are used alongside it. However, it’s much easier and less prone to fatal errors if developers hash their passwords with an option that is secure by default, like bcrypt, Argon2 or scrypt. Because of these issues, the National Institute of Standards and Technology no longer recommends MD5 for password hashing.
Data verification
MD5 also has applications in data verification, but before we discuss its merits, it’s important to understand the different types of data verification. One type of data verification involves verifying data for its integrity to determine whether it has accidentally become corrupted. By corrupted, we are talking about whether the data has been changed unintentionally, introducing errors. It can happen in a number of innocent ways, including:
- Bugs in software.
- Data transmission errors.
- Problems with the storage medium.
- Write errors that occurred while the files were being moved or copied.
If data becomes corrupted, it may no longer function as intended. Users may get an error when they try to access it, or portions of the information may have been lost.
In many situations, we also need to be able to verify data for its authenticity. By this, we mean that we need to verify that data hasn’t been secretly altered while it was in storage or in transit.
As an example, hackers often modify data to introduce malware, then attempt to pass it off as the benign original. Unwitting people may download it, thinking that it’s something harmless, then end up having to battle a virus that was secretly hidden inside.
Both integrity verification and authenticity verification have their roles. People may want to search their system for corrupted files to make sure they haven’t lost any data. In this case, they would want to verify the integrity of a file. On the other hand, when downloading a program from the internet, it’s a good idea to check the authenticity of the data to make sure that it has not been altered by hackers.
Cryptographic hash functions can be used for both integrity verification and authenticity verification, but MD5 is only suitable for integrity verification.
MD5 data integrity verification
In these situations, the MD5 hash function can be used as a checksum function. The underlying principle is that every file is run through the MD5 checksum function to produce a corresponding MD5 hash.
The files are run through the function periodically, each time producing hashes. As we discussed, cryptographic hash functions like MD5 are deterministic, and the output for a given input is always the same. Even minor changes to the input result in a radically different hash.
These properties enable us to compare the hashes of files over time. If the hashed output of a file is the same as it was at the start, then we know that the data has not become corrupted since it was first hashed.
If even a small amount of the data had been changed or altered over time, we will see a very different hash. This alerts us of the corruption, which means that we can take steps to try to recover the data, or replace it with a version from a previous backup.
While it is true that MD5 is weak against collision attacks, this doesn’t present much of a problem when using the algorithm as a checksum to verify data integrity. It is possible for two separate files to have the same hash value, but the likelihood of a file becoming corrupted in such a specific way that it still produces the same hash is so unlikely that it isn’t worth worrying about.
The problems with MD5 and data authentication
In cases where data may have been maliciously altered, MD5 isn’t secure to use because it isn’t collision resistant. If MD5 is used, file creators can try the same technique discussed in the Collision-resistant cryptographic hash functions section to produce two different files with the exact same hash. One of these could be legitimate, while the other is malicious.
If you downloaded a file and checked it against the original MD5 hash, you wouldn’t be able to tell whether it was the legitimate or malicious version. The hash would match in both cases. This means that MD5 cannot be relied upon to prove the authenticity of data.
For similar reasons, MD5 is unsuitable in other applications where authentication is required, such as in digital signatures and SSL certificates. In cases where you want to verify the authenticity of data and ensure that it has not been tampered with, it’s best to use a collision-resistant hash function like SHA-256 instead of the insecure MD5.
File identification with MD5
MD5 can be used for file identification in situations where there is limited risk from attackers manipulating files and causing collisions. If you want to attach a unique hash for easily identifying each file, you don’t have to worry too much about collisions. The chance of two of your files having the same hash identifier is so low that you shouldn’t be concerned.
Proof-of-work
With the increasing popularity of blockchain projects and cryptocurrencies, these technologies may be one of the most common areas where the layperson encounters hashing. Hash functions are essential for proof-of-work schemes, which verify cryptocurrency transactions while also mining new coins.
This process is accomplished by computers competing with each other to show that they have done the “work,” which really means they have run through a hash function countless times with different inputs, in order to find the input that produces a hash with a set number of zeros.
MD5 is unsuitable for the proof-of-work system used in Bitcoin, because it is simply too fast. If MD5 was Bitcoin’s hash function, miners would find the correct result too quickly and the block time would be much more rapid than the preferred time of around 10 minutes. Instead, SHA-256 is used as Bitcoin’s hash function.
Alternatives to MD5
With MD5’s security issues in mind, it is no longer appropriate in any situation where collision resistance is required. In most cases, SHA-256 or its relatives (SHA-224, SHA-384, SHA-512, SHA-512/224, SHA-512/256) are recommended instead.
The SHA-3 family of hash algorithms were released by NIST in 2015. However, it has not yet seen widespread adoption because SHA-256 and its relatives are still considered secure. Over time, we expect to see more serious attacks succeeding against SHA-256.
When these become more practical, the tech community will slowly move toward more secure hashing functions. But just as we have seen with MD5, it’s likely that a number of developers will continue using older algorithms in unsafe ways, long after we know of the security issues.
We’ve known of MD5’s problems for a long time now, so those that continue to use it in insecure ways have no excuse. In these cases, it poses a grave threat and should be rectified as soon as possible. If you come across a provider that still relies on MD5 for security, it’s probably best to switch to a competitor, because who knows what other poor practices they have in place.