We’ve been hiding messages for as long as we’ve been sending messages. The original ploy was to use fast and stealthy messengers to carry messages back and forth. Keeping messages away from prying eyes required evading capture.
If the messengers were caught, the message contents would be readable by the bad guys — who could take appropriate action. Sometimes this involved pretending to be the intended recipient and sending a false reply — thus executing the original Man In The Middle (MITM) attack.
The obvious solution to this was to somehow disguise the message’s true contents. If a message of this type were intercepted, the bad guy would be unable to read it and extract any useful information. The art of concealing the content of a message became known as cryptography which is a portmanteau of the Greek words for hidden and writing.
The methods of encrypting text are as limitless as our imaginations. However, the practical applications of any given encryption method are very limited. The methods to encrypt and decrypt must be known to both parties and they must be rigorous enough that the methods cannot be guessed by the bad guys. These two seemingly simple issues have continuously plagued encryption systems. The game of keeping encryption ciphers working against the never-ending onslaught of those seeking to break them has led to a rich and interesting history of ciphers.
Introduction to Cipher Terminology
Cryptography is a rich topic with a very interesting history and future. To get the most out of this article, it’s best to have a basic grip on a few terms and concepts. The next section will help with that. Feel free to skip it and come back to it if the need arises.
Block Cipher
A block cipher encrypts a message in a set number of bits (a block) at a time.
Code
Codes are more complex substitutions than a cipher in that codes transfer meaning rather than straight text substitution, e.g. The eagle has landed
. Code operations require a reference of some kind, usually referred to as a Code Book. Due to the cumbersome nature of transporting and maintaining code books, codes have fallen out of general use in modern cryptography in favour of ciphers.
Cipher
Ciphers are substitution of plaintext for ciphertext. No meaning is ascribed to the process, it is a mathematical or mechanical operation designed to simply obfuscate the plaintext. EG: the “rotation 13” algorithm (ROT13) where letters are assigned the letter 13 spots after it in the alphabet. This results in A=N, B=O, etc. To encrypt or decrypt a message, a person need only know the algorithm.
Cipher Text
Ciphertext is the unreadable, encrypted form of plaintext. Anyone attempting to read ciphertext will need to decode it first. Decoding ciphertext reveals the readable plaintext.
Keyspace
The number of possible keys that could have been used to create the ciphertext. Theoretically, difficulty in brute forcing ciphertext becomes more difficult as the keyspace increases.
Hash
A hash is a cipher that is used to provide a fingerprint of some data rather than a cipher text of that data. Hash ciphers take some message as input and output a predictable fingerprint based on that message. If the message is changed in any way, no matter how trivial, the fingerprint should differ dramatically. The most common use of hashes is to verify that a local copy of some file is a true reproduction of the original file.
The hallmarks of a good hashing cipher are:
- It is
deterministic
; meaning that the same message run through the same hash cipher will always produce the same fingerprint, and - It has a low level of
collision
; meaning that different messages run through the same hash cipher should produce a different fingerprint.
Monoalphabetic Ciphers
A cipher that uses a single alphabet and is usually a simple transposition. For example, the the letter A will be represented by the letter F.
These are so easily broken that we have cryptogram
books in drugstores alongside the crosswords for fun now.
Some examples of Monoalphabetic ciphers are:
- Caesar cipher
- Pigpen cipher
- Playfair cipher
- Morse code (despite its name)
Plain Text
Plaintext refers to the readable text of a message. Plaintext is encrypted into ciphertext and can be decrypted by the recipient back into plaintext.
Polyalphabetic Ciphers
This is a transpositional cipher, but unlike the monoalphabetic ciphers, more than one alphabet is used. There are signals embedded in the ciphertext which tell the recipient when the alphabet has changed.
Some examples of Polyalphabetic ciphers are:
- Alberti cipher
- Vigenère cipher
Stream Cipher
A stream cipher encrypts a message one character at a time. The Enigma machine is an example of a stream cipher.
Symmetric/Asymmetric Keys
In all but the most trivial encryption systems, a key is needed to encrypt and decrypt messages. If the same key is used for both purposes, then that key is referred to as symmetric. If different keys are used to encrypt and decrypt, as is the case with Public Key Cryptography, then the keys are said to be asymmetrical.
Symmetrical keys are generally considered slightly stronger than asymmetrical keys. But, they have the burden of needing a secure method in which to transfer the keys to all message participants in advance of use.
Cryptanalysis
There are two ways to discover the plaintext from the ciphertext. The first way is to decrypt the ciphertext using the expected decryption techniques. The second way is to use analysis to discover the plaintext without having possession of the encryption key. The latter process is colloquially referred to as breaking crypto which is more properly referred to as cryptanalysis.
Frequency Analysis
Cryptanalysis inspects the ciphertext and tries to find patterns or other indicators to reveal the plaintext beneath. The most commonly used cryptanalysis technique is frequency analysis. In the English language, there are 26 letters and the frequency of letters in common language is known. Vowels such as A and E turn up more frequently than letters such as Z and Q. Taking one step further back, entire words like THE and AN show up more frequently than words like ANT or BLUE.
To combat against word frequency, ciphertext can be broken up into standard blocks rather than left in their natural form. For example:
If we take the plaintext:
HOW MUCH WOOD WOULD A WOOD CHUCK CHUCK IF A WOOD CHUCK COULD CHUCK WOOD
and apply a Caesar Cipher that replaces each plaintext letter with a letter 16 positions along the alphabet, we get the following:
XEM CKSX MEET MEKBT Q MEET SXKSA SXKSA YV Q MEET SXKSA SEKBT SXKSA MEET
Extracting meaning
Frequency analysis gives us some clues as to the plaintext:
- The phrases MEET and SXKSA show up repeatedly
- The letters Q show up alone twice which is a strong indicator that Q is either an A or an I
- The word MEET is almost certain to have two vowels in the middle because there would be very few words with two of the same consonants in that position.
- A flaw in rotational ciphers is that no letter can equal itself, therefore we can eliminate the actual word MEET as plaintext.
- If we assume that Q is either an A or an I, then we can also assume that E is not either an A or an I and it can’t be an E. Since we’re pretty sure E is a vowel, that leaves us with E being either O or U. From there it takes little effort to test those options and eventually end up with a likely word
WOOD. - If
WOODis correct, then we can change the same letters in other words: E=0, M=W, T=D, Q=A, and continue on working our way through the ciphertext. - Another way to proceed would be to test if this is a simple rotation cipher. To do that, we would calculate the offset from a ciphertext letter and a plaintext letter such as M = W. That gives us 16, and if we then reverse every letter back 16 slots in the alphabet, the rest of the plaintext will either make sense, or it will still be unintelligible gibberish.
Using standard blocks
Now consider the same example if standard blocks of four are used. The ciphertext would look like this:
XEMCK SXMEE TMEKB TQMEE TSXKS ASXKS AYVQM EETSX KSASE KBTSX KSAME ET
While this does not make frequency analysis impossible, it makes it much harder. The first step in tackling this type of cipher would be to attempt to break it back into its natural wording. It’s still possible to see repetitions like MEET and SXKSA but it’s much more difficult to pick out standalone words such as what the Q represents.
If you like this type of thing, check out your local drugstore or book store’s magazine section. There are usually crypto game books in the same section as the crossword books. The FBI website also has some cryptoanalysis challenges.
Use of Superseded Cryptographic Keys
In modern use, cryptography keys can be expired and replaced. In large systems such as those used by the military, cryptographic keys are replaced at set times: hourly, daily, weekly, monthly, or yearly. When a key is replaced, the previous key is said to be superseded.
Superseded keys must be destroyed because they present an extremely valuable cryptanalysis tool. If an adversary has collected and stockpiled encrypted communications and can later decrypt those communications by gaining the superseded key used to encrypt them, that provides fertile ground for cryptanalysis of current day messages.
On the commercial internet in a post-Snowden era, it’s easy to imagine the NSA obtaining superseded SSL keys and going back to decrypt the vast trove of data obtained through programs like PRISM.
Quantum computing and cryptanalysis
Today’s computers have not changed significantly since inception. At the fundamental level, computers operate on bits which are single slots which can contain either the value 1 or the value 0. Every process that takes place on a computer, including the encryption and decryption of messages, needs to be boiled down to that simple foundation.
By contrast, quantum computers operate using the physics concepts of superposition and entanglement instead of bits to compute. If proven feasible, quantum computing would likely be able to break any modern crypto system in a fraction of the time it takes today. Conversely, quantum computing should also be able to support new types of encryption which would usher in an entirely new era of cryptography.
Historical progression
Initial monoalphabetic and polyalphabetic ciphers had the same problem: they used a static, never changing key. This is a problem because once an adversary understood how to lay out a pigpen diagram, for example, she could decrypt every single message ever encrypted with that algorithm.
Encryption keys
In order to obfuscate the text more, the concept of changing keys was developed. Using the Caesar Cipher, one could change the ciphertext by simply incrementing the value of the rotation. For example:
Using the Caesar Cipher to encrypt the phrase FLEE TO THE HILLS FOR ALL IS LOST
Rotation of 10 ciphertext:
PVOO DY DRO RSVVC PYB KVV SC VYCD
Rotation of 4 ciphertext:
JPII XS XLI LMPPW JSV EPP MW PSWXThe advantage of applying an arbitrary key to the plaintext is that someone who knows how the Caesar Cipher works would still not be able to decrypt the text without knowing what rotational value was used to encrypt it.
While the example above is a simple example due to the trivial nature of the Caesar Cipher to begin with, applying more complex keys can rigorously increase the security of ciphertext.
Significant Ciphers
Throughout history there have been many types of ciphers. They primarily began as a military tool. Indeed, militaries are still the heaviest users of cryptography today. In order to be militarily successful, a cipher has to have these attributes:
- resistance to cryptanalysis
- flexible enough to transport by messenger across rough conditions
- easy to use on a muddy, bloody battlefield
Any cipher that was prone to error in encrypting or decrypting on the battlefield or fell too easily to interception and inspection did not last long. Keep in mind that one error in encryption can render an entire message completely unreadable by the recipient.
Some of the more notable ciphers follow in the next section.
Scytale – 120 AD
This is a monoalphabetic, symmetrical cipher system. The sender and receiver must both be in possession of a cylinder of wood exactly the same diameter. In effect, this is the key
.
The sender takes a long narrow piece of fabric and coils it around the scytale. He then writes the message in standard right-to-left format on the fabric. The fabric is then removed from the scytale and looks to be just a long strip of cloth which can be scrunched up and hidden in the smallest of places for transport.

The recipient simply need to wrap the fabric around their matching scytale and the message becomes clear. While this simple cipher would fall very quickly to cryptanalysis, the premise is that only a scytale of exactly the same diameter could decrypt the message.
Vigenère – 1553
Originally described by Giovan Bellaso in 1553, the Vigenère cipher was misattributed in the 19th century to Blaise de Vigenère. The Vigenère cipher is one of the first polyalphabetic ciphers. It is still symmetrical in nature, but it was tough enough to crack that it remained in use for over three centuries.
Polyalphabetic ciphers allow the use of many alphabets during encryption, which greatly increases the keyspace of the ciphertext. Earlier versions of polyalphabetic ciphers required rigid adherence to the spots at which the alphabet would change. Bellaso’s implementation of this cipher allowed the sender to change alphabets at arbitrary spots in the encryption process. The signal of an alphabet change had to be agreed upon in advance between the sender and receiver, therefore this is still a symmetrical method of encryption.

The Vigenère cipher was used in practise as recently as the American Civil War. However, it’s well understood that the Union repeatedly broke those messages because the Confederacy leadership relied heavily on too few key phrases to signal alphabet changes.
Pigpen Cipher – 1700’s
Also known as the Freemason’s Cipher, the Pigpen Cipher is another symmetrical monoalphabetic substitution cipher. Encrypt and decryption is done by laying out 4 grids. Two grids contain 9 spaces like a tic-tac-toe board, and two grids resemble a large letter X and contain 4 spaces each. Together, there are 26 spaces to coincide with the 26 letters in the Latin alphabet. The sections are all uniquely identifiable by a combination of the shape of the section and the presence, or absence, of a dot in it. Messages are encrypted by using the section identifier instead of the actual letter.
I’ve created a Pigpen cipher key here:
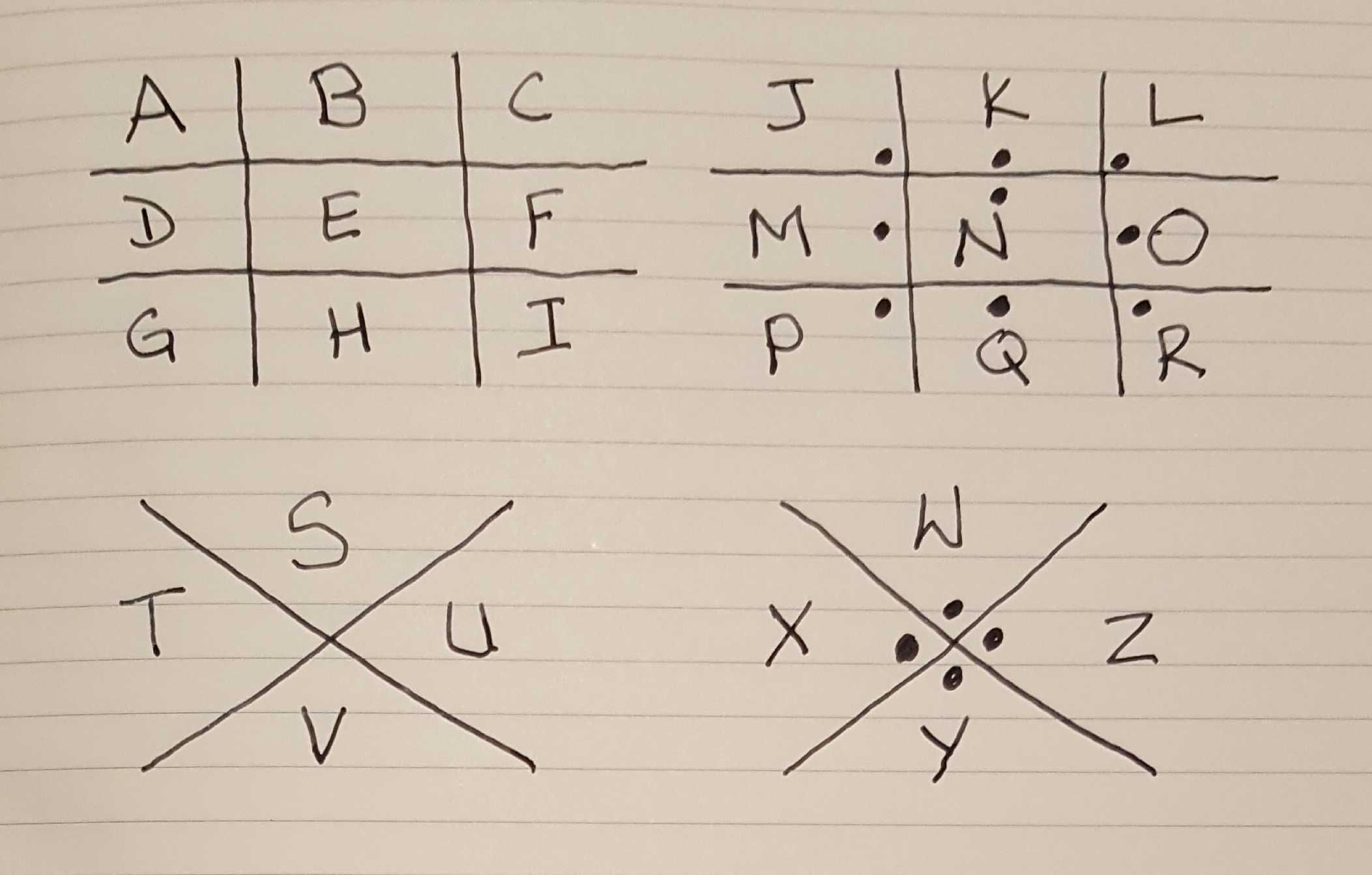
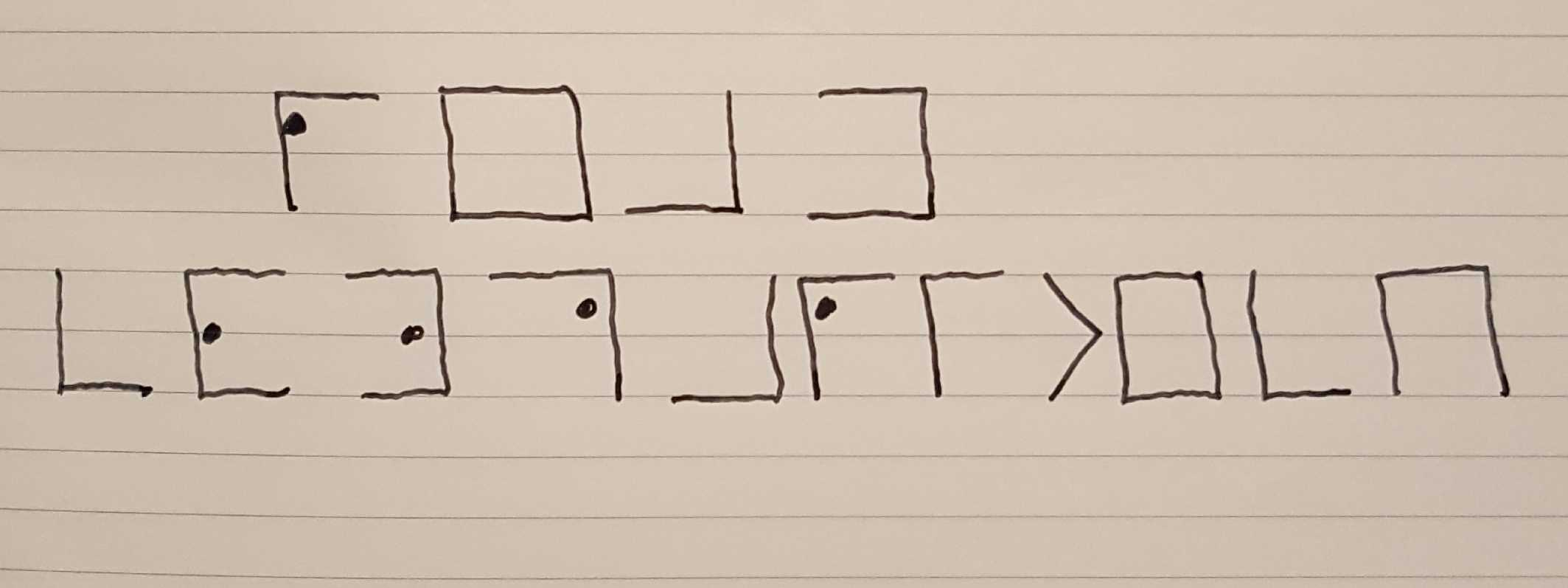
Decryption is done by laying out the same grid, and transposing back the section identifier to the letter. Therefore, a plaintext phrase of READ COMPARITECH
encrypts into this series of images:
Playfair cipher – 1854
The Playfair cipher uses 26 bi-grams (two letters) instead of 26 monograms as the encoding key. This vastly increases the keyspace of the ciphertext and makes frequency analysis very difficult.
Playfair-encoded messages are created by constructing a 5×5 grid of letters which is generated by a random short phrase, and then filling in the rest of the grid with non-repeating letters from the alphabet. That grid forms the key and anyone wishing to decrypt the message must reconstruct this same grid. The recipient must also know the same short phrase used to encrypt the message which is much harder to determine than a simple rotational number.
Astute readers will realize that 5 x 5 = 25, but there are 26 letters in the Latin alphabet. To accommodate this, the letters I and J are usually used interchangeably. Any two other letters could be used as well, but that information would have to be communicated to the recipient to ensure they decoded the message properly.
Playfair in action
Once the grid was constructed, users only had to know 4 simple rules to encrypt or decrypt the message. It’s difficult to make sense of the key in a written article so I created a Playfair grid to illustrate. I’ve used the phrase READ COMPARITECH
as the key phrase. After writing that out, I start writing the alphabet to fill in the rest of the grid. Remember that each letter can only be in the grid once and I and J are interchangeable. That gives me a Playfair key like the image below. The letters in red were omitted because they already appear in the grid.

Keep in mind that the phase READ COMPARITECH
is just the random phrase to build the grid. It is not the encrypted text. This resulting grid would be used to encrypt your plaintext.
One time pads (OTP) – 1882
A One Time Pad (OTP) refers to a symmetric encryption system using keys that are changed with every single message. If the keys truly are one time
, then ciphertext would be extremely resistant to cryptanalysis. These keys were literally written on pads of paper originally and since each key is only used once, the name One Time Pad stuck.
In practice, OTP is hard to deploy properly. As a symmetrical system, it requires the sender and all the recipients to have the same OTP book. It also has a significant disadvantage in that a message cannot be longer than the pad in use. If it were, then parts of the pad would have to be re-used, which significantly weakens the ciphertext to cryptanalysis.
OTPs are still in use today in some militaries for quick, tactical field messages.
Engima – 1914
Created by German citizen Arthur Scherbius after WW1 for commercial purposes, the Enigma machine is a polyalphabetic stream cipher machine. The machine consisted of a keyboard, a light panel and some adjustable rotors.
Operators would set the position of the rotors and then type a message on the keypad. As each letter was typed, a corresponding letter would illuminate on the light pad. This was the encrypted letter that formed the ciphertext. Receivers would have to know the correct rotors settings to use, and then they perform the same process. However, as the receiver typed in each letter of ciphertext, the corresponding letter that would illuminate would be the plaintext letter.

The German military enhanced the machine by adding a plugboard and therefore considered it unbreakable and used the Enigma for everything. The Polish General Staff’s Cipher Bureau broke the Germany military Enigma in 1932. They were able to reverse engineer the machine from information derived by the poor operational security (OpSec) of German Enigma users. However, they were unable to actually decrypt messages until the French shared Enigma information gleaned from one of their German spies.
The Polish Policy Cipher Bureau was able to read German Enigma traffic for years until the German’s continued advances in the system made it too difficult. At that point, just before the outbreak of WWII, the UK and France were brought into the fold and the monitoring and decryption of Enigma traffic became part of Project Ultra.
It is generally accepted that the Allies’ ability to decrypt Enigma traffic shortened the outcome of WWII by several years.
SHA Family Hash Ciphers 1993 – 2012
SHA is a family of algorithms which are used for hashing rather than encryption and published by the National Institute of Standards and Technology (NIST). The original SHA cipher published in 1993 is now designated SHA-0 in order to fit in with the naming conventions of subsequent versions.
Both SHA-0 and SHA-1 (retired in 2010) have been shown to be unable to meet the standard hash hallmarks (listed in the terminology section) and are no longer in use. HMAC-SHA1 is still considered unbroken but SHA-1 in all flavours should be discarded in favour of higher versions where practical.
Current SHA ciphers SHA-2 and SHA-3 (2012) are both still in use today.
MD5 Hash – 1991
MD5 is a hashing algorithm developed in 1991 to address security issues — such as the ease of collision attacks — in MD4. By 2004 MD5 had essentially been broken by a crowd-sourcing effort showing that MD5 was very vulnerable to a Birthday Attack.
MD5 fingerprints are still provided today for file or message validation. But since it is cryptographically broken, MD5 hashes can only be relied upon to detect unintentional file or message changes. Intentional changes can be masked due to the weakness of the algorithm.
Modern Ciphers
Cryptography is in wide use on the internet today. A great deal of our internet activities are encrypted using TLS (Transport Layer Security) and keys are exchanged using an asymmetrical process.
Computers are exceptionally good at processing data using algorithms. Once computers arrived on the scene, cipher development exploded. Computers are not only an excellent tool for creating cryptographic ciphers, they’re also exceptionally useful for breaking cryptographic ciphers via cryptanalysis. This means that increases in computer power are always heralded by new ciphers being developed and old ciphers being retired because they are now too easy to break.
Due to this never-ending battle of computing power, computers using the internet usually support a large list of ciphers at any given time. This list of ciphers is called a cipher suite and when two computers connect, they share the list of ciphers they both support and a common cipher is agreed upon in order to carry out encryption between them. This process exists to ensure the greatest interoperability between users and servers at any given time.
Ciphers such as the Enigma and DES (Data Encryption Standard) have been broken and are no longer considered safe for cryptographic use. To date, RSA (Rivest, Shamir, Adleman) and AES (Advanced Encryption Standard) are considered safe, but as computing power increases, those will also fall one day and new ciphers will have to be developed to continue the use of cryptography on the web.
Public key cryptography
Public key cryptography is an asymmetrical system in wide use today by people and computers alike. The key used to encrypt data — but not decrypt it — is called the public key. Every recipient has their own public key which is made widely available. Senders must use the public key of the intended recipient to encode the message. Then the recipient can use their companion secret key called the private key to decrypt the message.
RSA is the underlying cipher used in public key cryptography. The RSA cipher multiplies two very large prime numbers together as part of the key generation process. Its strength relies on the fact that an adversary would have to correctly factor that product into the two prime numbers originally used. Even with today’s computing power that is not feasible in most cases. You may recall that factorization is the process of reducing a number to the two smallest numbers that can be multiplied together to produce the original number. Prime numbers have only two factors, 1 and themselves.
Asymmetrical ciphers are slower than symmetrical ciphers, but the public key implementation of asymmetrical crypto has one distinct advantage: since the public key cannot be used to decrypt messages, it can be communicated to the sender without any safeguards. Thus, there is no need for the two parties to exchange keys prior to exchanging their first encrypted message.
For small things like emails, asymmetrical cryptography is fine. However, for large scale encryption — such as entire disks or file backups — it is too slow. Most large-scale crypto systems today use a hybrid approach; asymmetrical crypto is used to exchange symmetrical keys, and then the symmetrical keys are used for the actual encryption and decryption processes.
Unbroken ciphertext
Given our computing power today, it may seem incredible to find out that there are some very old ciphertexts that have not yet been decrypted.
The final Zodiac Killer’s Letter
The Zodiac Killer was a serial killer that terrorized California for several years in the late 60’s. The killer sent four cipher messages to Bay Area newspapers — the first of which was cracked in a week. The second 340-character cipher took 51 years to solve. The final two ciphers consist of 13 and 32 characters and are deemed too short to have a unique solution.
Three final Enigma messages
Not all Enigma messages have been decrypted yet. While there’s little military value in doing so, there is an Enigma @ Home project that seeks to decrypt the few remaining messages from 1942. Much like other @ home
projects such as SETI @ Home, the project uses spare CPU cycles on members’ computers to attempt to decrypt the final messages.
What’s Next?
Computing is still a young science. We’re still operating off of “version 1”, meaning that our computers are still limited to the binary ones-and-zeros functions. Quantum computing is likely the next big thing in computing. It will fundamentally change how computing works — as opposed to the current approach of just increasing processing power to handle more ones and zeroes. Quantum mechanics has a strange properly called the “superposition”, which means that something can be in more than one state until it is observed. The most famous thought experiment that illustrates superposition is that of Schrodinger’s Cat, where the cat in a box is both alive and dead until it collapses into one of those states upon being observed.
In computing this means that qubits (quantum bits) can have two states instead of binary’s one state. While a bit can only be 1 or 0, a qubit can be both via the concept of superposition. Not only does this make hard math such as that used to factor large numbers almost trivial to perform, it also may herald the end of Man-In-The-Middle attacks.
Another property of quantum transmission is the concept of “interference”. Interference is the behavior of subatomic electrons to pass through a barrier and then reconvene on the other side. Interference can only take place if nobody observes it (tree, forest, anyone?). It would therefore be theoretically impossible for someone to intercept a message passed through a quantum system without being discovered. The path of the electrons would be changed by being observed and interference would no longer occur, thus indicating the message has been observed.
Counting qubits
In 2022, IBM unveiled a quantum computer with 433 qubits. This was more than triple the size of the machine it broke records with just a year before. In 2023, the company announced it was aiming to build a 100,000-qubit machine within a decade.
To threaten 2048-bit RSA encryption, researchers have shown that a quantum computer with 20 million qubits would be needed. However, by the time this is achievable, the cryptographic world will have moved on. Indeed, NIST has a selection of algorithms for post-quantum cryptography.
Image credit: “Scytale” by Lurigen. CC Share-A-Like 3.0

